Summary
The FMZ platform launched a trading factor analysis tool based on “WorldQuant Alpha101”, which provides a new weapon for developers of quantitative trading strategies. Through analysis factors, it helps everyone better understand the market and gain insight into the opportunities behind the financial market.
What is Alpha101

Before introducing Alpha101, first understand what is Alpha? Alpha refers to excess returns. For example: buy 1 million index fund and keep it all the time. This is a Beta strategy to earn passive returns in the market. But if you use 10 million to buy 10 stocks, and earn 10% more by buying an index fund, then this 10% is Alpha excess returns. Don’t underestimate this Alpha excess return. In fact, most traders in the market, including fund managers, can’t beat the index, so many people rack their brains to improve Alpha’s return. Of course, there are some excellent traders and fund companies.
- Trading strategy excess return = passive (Beta) return + trading (Alpha) return
In 2015, the “WorldQuant LLC” quantitative trading hedge fund, which is good at data mining, released the “WorldQuant Formulaic 101 Alphas” research report, which disclosed the 101 Alpha expressions they are or have used, whose purpose is to give trading strategy developers Provide more inspiration and ideas. Many people questioned the factors disclosed by WorldQuant, because after all, the Chinese stock market is different from foreign stock markets. But it turns out that most of these factors are still effective in the Chinese market. FMZ platform reduplicated and corrected of these factor formulas, and showed it to all traders.
What are the factors in Alpha101
In the research report, Alpha is divided into three categories: price factor, volume factor, and dichotomy factor.
- Price factor: The calculation formula only uses the price, including: opening price, highest price, lowest price, closing price, etc. The output is a specific value.
- Volume and price factor: The calculation formula uses volume and price. The design idea is to determine the relationship between price changes and trading volume changes, and the output is a specific value.
- Dichotomy factor: The calculation formula uses trading volume and price. It is the same as the volume and price factor, except that the output is 0 or 1.
Price factor
| Factor name | Factor formula | FMZ Notes |
|---|---|---|
| Alpha#1 | (rank(ts*argmax(signedpower(((returns < 0) ? stddev(returns, 20) : close), 2.), 5)) – 0.5) | Trend |
| Alpha#4 | (-1 * ts_rank(rank(low), 9)) | Reverse |
| Alpha#5 | (rank((open – (sum(vwap, 10) / 10))) * (-1 _ abs(rank((close – vwap))))) | Reverse |
| Alpha#8 | (-1 _ rank(((sum(open, 5) _ sum(returns, 5)) – delay((sum(open, 5) * sum(returns, 5)), 10)))) | Reverse |
| Alpha#9 | ((0 < ts*min(delta(close, 1), 5)) ? delta(close, 1) : ((ts_max(delta(close, 1), 5) < 0) ? delta(close, 1) : (-1 * delta(close, 1)))) | Reverse or Trend |
| Alpha#18 | (-1 * rank(((stddev(abs((close – open)), 5) + (close – open)) + correlation(close, open, 10)))) | Reverse |
| Alpha#19 | ((-1 * sign(((close – delay(close, 7)) + delta(close, 7)))) _ (1 + rank((1 + sum(returns, 250))))) | Trend Divergence |
| Alpha#20 | (((-1 * rank((open – delay(high, 1)))) _ rank((open – delay(close, 1)))) * rank((open – delay(low, 1)))) | Reverse |
| Alpha#23 | (((sum(high, 20) / 20) < high) ? (-1 * delta(high, 2)) : 0) | Short-term regression on the 20-period moving average |
| Alpha#24 | ((((delta((sum(close, 100) / 100), 100) / delay(close, 100)) < 0.05) 或 ((delta((sum(close, 100) / 100), 100) / delay(close, 100)) == 0.05)) ? (-1 _ (close – ts_min(close, 100))) : (-1 _ delta(close, 3))) | Reverse |
| Alpha#29 | (min(product(rank(rank(scale(log(sum(tsmin(rank(rank((-1 * rank(delta((close – 1), 5))))), 2), 1))))), 1), 5) + tsrank(delay((-1 * returns), 6), 5)) | Reverse |
| Alpha#32 | (scale(((sum(close, 7) / 7) – close)) + (20 * scale(correlation(vwap, delay(close, 5), 230)))) | Reverse |
| Alpha#33 | rank((-1 * ((1 – (open / close))^1))) | Reverse |
| Alpha#34 | rank(((1 – rank((stddev(returns, 2) / stddev(returns, 5)))) + (1 – rank(delta(close, 1))))) | Reverse |
| Alpha#37 | (rank(correlation(delay((open – close), 1), close, 200)) + rank((open – close))) | Statistics |
| Alpha#38 | ((-1 _ rank(ts_rank(close, 10))) _ rank((close / open))) | Reverse |
| Alpha#41 | (((high * low)^0.5) – vwap) | Reverse |
| Alpha#42 | (rank((vwap – close)) / rank((vwap + close))) | Reverse |
| Alpha#46 | ((0.25 < (((delay(close, 20) – delay(close, 10)) / 10) – ((delay(close, 10) – close) / 10))) ? (-1 _ 1) : (((((delay(close, 20) – delay(close, 10)) / 10) – ((delay(close, 10) – close) / 10)) < 0) ? 1 : ((-1 _ 1) * (close – delay(close, 1))))) | Reverse |
| Alpha#48 | Undone | Undone |
| Alpha#49 | (((((delay(close, 20) – delay(close, 10)) / 10) – ((delay(close, 10) – close) / 10)) < (-1 _ 0.1)) ? 1 : ((-1 _ 1) * (close – delay(close, 1)))) | Reverse |
| Alpha#51 | (((((delay(close, 20) – delay(close, 10)) / 10) – ((delay(close, 10) – close) / 10)) < (-1 _ 0.05)) ? 1 : ((-1 _ 1) * (close – delay(close, 1)))) | None |
| Alpha#53 | (-1 * delta((((close – low) – (high – close)) / (close – low)), 9)) | Reverse |
| Alpha#54 | ((-1 _ ((low – close) _ (open^5))) / ((low – high) * (close^5))) | Reverse |
| Alpha#56 | Undone | Undone |
| Alpha#57 | (0 – (1 * ((close – vwap) / decay*linear(rank(ts_argmax(close, 30)), 2)))) | Reverse |
| Alpha#60 | (0 – (1 * ((2 _ scale(rank(((((close – low) – (high – close)) / (high – low)) * volume)))) – scale(rank(ts*argmax(close, 10)))))) | None |
| Alpha#66 | ((rank(decay_linear(delta(vwap, 3.51013), 7.23052)) + ts_rank(decay_linear(((((low * 0.96633) + (low _ (1 – 0.96633))) – vwap) / (open – ((high + low) / 2))), 11.4157), 6.72611)) * -1) | Reverse |
| Alpha#73 | (max(rank(decay*linear(delta(vwap, 4.72775), 2.91864)), ts_rank(decay_linear(((delta(((open * 0.147155) + (low _ (1 – 0.147155))), 2.03608) / ((open _ 0.147155) + (low _ (1 – 0.147155)))) _ -1), 3.33829), 16.7411)) _ -1) | Reverse |
| Alpha#84 | signedpower(ts_rank((vwap – ts_max(vwap, 15.3217)), 20.7127), delta(close, 4.96796)) | None |
| Alpha#101 | ((close – open) / ((high – low) + .001)) | Reverse |
Volume-price Factor
| Factor name | Factor formula | FMZ Notes |
|---|---|---|
| Alpha#2 | (-1 * correlation(rank(delta(log(volume), 2)), rank(((close – open) / open)), 6)) | Volume and price divergence |
| Alpha#3 | (-1 * correlation(rank(open), rank(volume), 10)) | Volume and price divergence |
| Alpha#6 | (-1 * correlation(open, volume, 10)) | Volume and price divergence |
| Alpha#7 | ((adv20 < volume) ? ((-1 _ ts_rank(abs(delta(close, 7)), 60)) _ sign(delta(close, 7))) : (-1 * 1)) | None |
| Alpha#11 | ((rank(ts*max((vwap – close), 3)) + rank(ts_min((vwap – close), 3))) * rank(delta(volume, 3))) | Reverse Shrinkage |
| Alpha#12 | (sign(delta(volume, 1)) * (-1 _ delta(close, 1))) | Volume and price divergence |
| Alpha#13 | (-1 * rank(covariance(rank(close), rank(volume), 5))) | Volume and price divergence |
| Alpha#14 | ((-1 _ rank(delta(returns, 3))) _ correlation(open, volume, 10)) | Volume and price divergence |
| Alpha#15 | (-1 * sum(rank(correlation(rank(high), rank(volume), 3)), 3)) | Volume and price divergence |
| Alpha#16 | (-1 * rank(covariance(rank(high), rank(volume), 5))) | Volume and price divergence |
| Alpha#17 | (((-1 _ rank(ts_rank(close, 10))) _ rank(delta(delta(close, 1), 1))) * rank(ts*rank((volume / adv20), 5))) | Reverse Shrinkage |
| Alpha#22 | (-1 * (delta(correlation(high, volume, 5), 5) _ rank(stddev(close, 20)))) | Volume and price divergence |
| Alpha#25 | rank(((((-1 _ returns) _ adv20) _ vwap) _ (high – close))) | None |
| Alpha#26 | (-1 * ts*max(correlation(ts_rank(volume, 5), ts_rank(high, 5), 5), 3)) | Volume and price divergence |
| Alpha#28 | scale(((correlation(adv20, low, 5) + ((high + low) / 2)) – close)) | Depart from Reverse |
| Alpha#30 | (((1.0 – rank(((sign((close – delay(close, 1))) + sign((delay(close, 1) – delay(close, 2)))) + sign((delay(close, 2) – delay(close, 3)))))) * sum(volume, 5)) / sum(volume, 20)) | Reverse |
| Alpha#31 | ((rank(rank(rank(decay_linear((-1 * rank(rank(delta(close, 10)))), 10)))) + rank((-1 _ delta(close, 3)))) + sign(scale(correlation(adv20, low, 12)))) | Volume and price divergenceReverse |
| Alpha#35 | ((tsrank(volume, 32) * (1 – tsrank(((close + high) – low), 16))) * (1 – ts*rank(returns, 32))) | None |
| Alpha#36 | (((((2.21 * rank(correlation((close – open), delay(volume, 1), 15))) + (0.7 _ rank((open – close)))) + (0.73 _ rank(ts*rank(delay((-1 * returns), 6), 5)))) + rank(abs(correlation(vwap, adv20, 6)))) + (0.6 _ rank((((sum(close, 200) / 200) – open) _ (close – open))))) | Trend |
| Alpha#39 | ((-1 _ rank((delta(close, 7) _ (1 – rank(decay*linear((volume / adv20), 9)))))) * (1 + rank(sum(returns, 250)))) | Volume and price divergenceReverse |
| Alpha#40 | ((-1 * rank(stddev(high, 10))) _ correlation(high, volume, 10)) | Volume and price divergence |
| Alpha#43 | (tsrank((volume / adv20), 20) * tsrank((-1 * delta(close, 7)), 8)) | Reverse Divergence |
| Alpha#44 | (-1 * correlation(high, rank(volume), 5)) | Volume and price divergence |
| Alpha#45 | (-1 _ ((rank((sum(delay(close, 5), 20) / 20)) _ correlation(close, volume, 2)) * rank(correlation(sum(close, 5), sum(close, 20), 2)))) | Volume and price divergence |
| Alpha#47 | ((((rank((1 / close)) _ volume) / adv20) _ ((high * rank((high – close))) / (sum(high, 5) / 5))) – rank((vwap – delay(vwap, 5)))) | None |
| Alpha#50 | (-1 * ts*max(rank(correlation(rank(volume), rank(vwap), 5)), 5)) | Volume and price divergence |
| Alpha#52 | ((((-1 * tsmin(low, 5)) + delay(ts_min(low, 5), 5)) * rank(((sum(returns, 240) – sum(returns, 20)) / 220))) * tsrank(volume, 5)) | Volume and price divergence |
| Alpha#55 | (-1 * correlation(rank(((close – ts_min(low, 12)) / (ts_max(high, 12) – ts_min(low, 12)))), rank(volume), 6)) | Volume and price divergence |
| Alpha#58 | Undone | Undone |
| Alpha#59 | Undone | Undone |
| Alpha#63 | Undone | Undone |
| Alpha#67 | Undone | Undone |
| Alpha#69 | Undone | Undone |
| Alpha#70 | Undone | Undone |
| Alpha#71 | max(ts_rank(decay_linear(correlation(ts_rank(close, 3.43976), ts_rank(adv180, 12.0647), 18.0175), 4.20501), 15.6948), ts_rank(decay_linear((rank(((low + open) – (vwap + vwap)))^2), 16.4662), 4.4388)) | None |
| Alpha#72 | (rank(decay_linear(correlation(((high + low) / 2), adv40, 8.93345), 10.1519)) / rank(decay_linear(correlation(ts_rank(vwap, 3.72469), ts_rank(volume, 18.5188), 6.86671), 2.95011))) | None |
| Alpha#76 | Undone | Undone |
| Alpha#77 | min(rank(decay_linear(((((high + low) / 2) + high) – (vwap + high)), 20.0451)), rank(decay_linear(correlation(((high + low) / 2), adv40, 3.1614), 5.64125))) | None |
| Alpha#78 | (rank(correlation(sum(((low * 0.352233) + (vwap _ (1 – 0.352233))), 19.7428), sum(adv40, 19.7428), 6.83313))^rank(correlation(rank(vwap), rank(volume), 5.77492))) | None |
| Alpha#80 | Undone | Undone |
| Alpha#82 | Undone | Undone |
| Alpha#83 | ((rank(delay(((high – low) / (sum(close, 5) / 5)), 2)) * rank(rank(volume))) / (((high – low) / (sum(close, 5) / 5)) / (vwap – close))) | None |
| Alpha#85 | (rank(correlation(((high _ 0.876703) + (close _ (1 – 0.876703))), adv30, 9.61331))^rank(correlation(ts_rank(((high + low) / 2), 3.70596), ts_rank(volume, 10.1595), 7.11408))) | None |
| Alpha#87 | Undone | Undone |
| Alpha#88 | min(rank(decay_linear(((rank(open) + rank(low)) – (rank(high) + rank(close))), 8.06882)), ts_rank(decay_linear(correlation(ts_rank(close, 8.44728), ts_rank(adv60, 20.6966), 8.01266), 6.65053), 2.61957)) | None |
| Alpha#89 | Undone | Undone |
| Alpha#90 | Undone | Undone |
| Alpha#91 | Undone | Undone |
| Alpha#92 | min(ts_rank(decay_linear(((((high + low) / 2) + close) < (low + open)), 14.7221), 18.8683), ts_rank(decay_linear(correlation(rank(low), rank(adv30), 7.58555), 6.94024), 6.80584)) | None |
| Alpha#93 | Undone | Undone |
| Alpha#94 | ((rank((vwap – ts_min(vwap, 11.5783)))^ts_rank(correlation(ts_rank(vwap, 19.6462), ts_rank(adv60, 4.02992), 18.0926), 2.70756)) * -1) | None |
| Alpha#96 | (max(ts_rank(decay_linear(correlation(rank(vwap), rank(volume), 3.83878), 4.16783), 8.38151), ts_rank(decay_linear(ts_argmax(correlation(ts_rank(close, 7.45404), ts_rank(adv60, 4.13242), 3.65459), 12.6556), 14.0365), 13.4143)) * -1) | None |
| Alpha#97 | Undone | Undone |
| Alpha#98 | (rank(decay_linear(correlation(vwap, sum(adv5, 26.4719), 4.58418), 7.18088)) – rank(decay_linear(ts_rank(ts_argmin(correlation(rank(open), rank(adv15), 20.8187), 8.62571), 6.95668), 8.07206))) | None |
| Alpha#100 | Undone | Undone |
Dichotomy Factor
| Factor name | Factor formula | FMZ Notes |
|---|---|---|
| Alpha#22 | (-1 _ (delta(correlation(high, volume, 5), 5) _ rank(stddev(close, 20)))) | Reverse |
| Alpha#27 | ((0.5 < rank((sum(correlation(rank(volume), rank(vwap), 6), 2) / 2.0))) ? (-1 * 1) : 1) | Volume and price divergence |
| Alpha#61 | (rank((vwap – ts*min(vwap, 16.1219))) < rank(correlation(vwap, adv180, 17.9282))) | Volume and price divergence |
| Alpha#62 | ((rank(correlation(vwap, sum(adv20, 22.4101), 9.91009)) < rank(((rank(open) + rank(open)) < (rank(((high + low) / 2)) + rank(high))))) * -1) | None |
| Alpha#64 | ((rank(correlation(sum(((open * 0.178404) + (low _ (1 – 0.178404))), 12.7054), sum(adv120, 12.7054), 16.6208)) < rank(delta(((((high + low) / 2) _ 0.178404) + (vwap _ (1 – 0.178404))), 3.69741))) * -1) | None |
| Alpha#65 | ((rank(correlation(((open _ 0.00817205) + (vwap _ (1 – 0.00817205))), sum(adv60, 8.6911), 6.40374)) < rank((open – ts*min(open, 13.635)))) * -1) | None |
| Alpha#68 | ((ts_rank(correlation(rank(high), rank(adv15), 8.91644), 13.9333) < rank(delta(((close * 0.518371) + (low _ (1 – 0.518371))), 1.06157))) * -1) | None |
| Alpha#74 | ((rank(correlation(close, sum(adv30, 37.4843), 15.1365)) < rank(correlation(rank(((high _ 0.0261661) + (vwap _ (1 – 0.0261661)))), rank(volume), 11.4791))) * -1) | None |
| Alpha#75 | (rank(correlation(vwap, volume, 4.24304)) < rank(correlation(rank(low), rank(adv50), 12.4413))) | Volume-price relationship |
| Alpha#79 | Undone | Undone |
| Alpha#81 | ((rank(log(product(rank((rank(correlation(vwap, sum(adv10, 49.6054), 8.47743))^4)), 14.9655))) < rank(correlation(rank(vwap), rank(volume), 5.07914))) * -1) | None |
| Alpha#86 | ((ts_rank(correlation(close, sum(adv20, 14.7444), 6.00049), 20.4195) < rank(((open + close) – (vwap + open)))) * -1) | None |
| Alpha#95 | (rank((open – ts_min(open, 12.4105))) < ts_rank((rank(correlation(sum(((high + low) / 2), 19.1351), sum(adv40, 19.1351), 12.8742))^5), 11.7584)) | None |
| Alpha#99 | ((rank(correlation(sum(((high + low) / 2), 19.8975), sum(adv60, 19.8975), 8.8136)) < rank(correlation(low, volume, 6.28259))) * -1) | None |
Implemented on FMZ platform
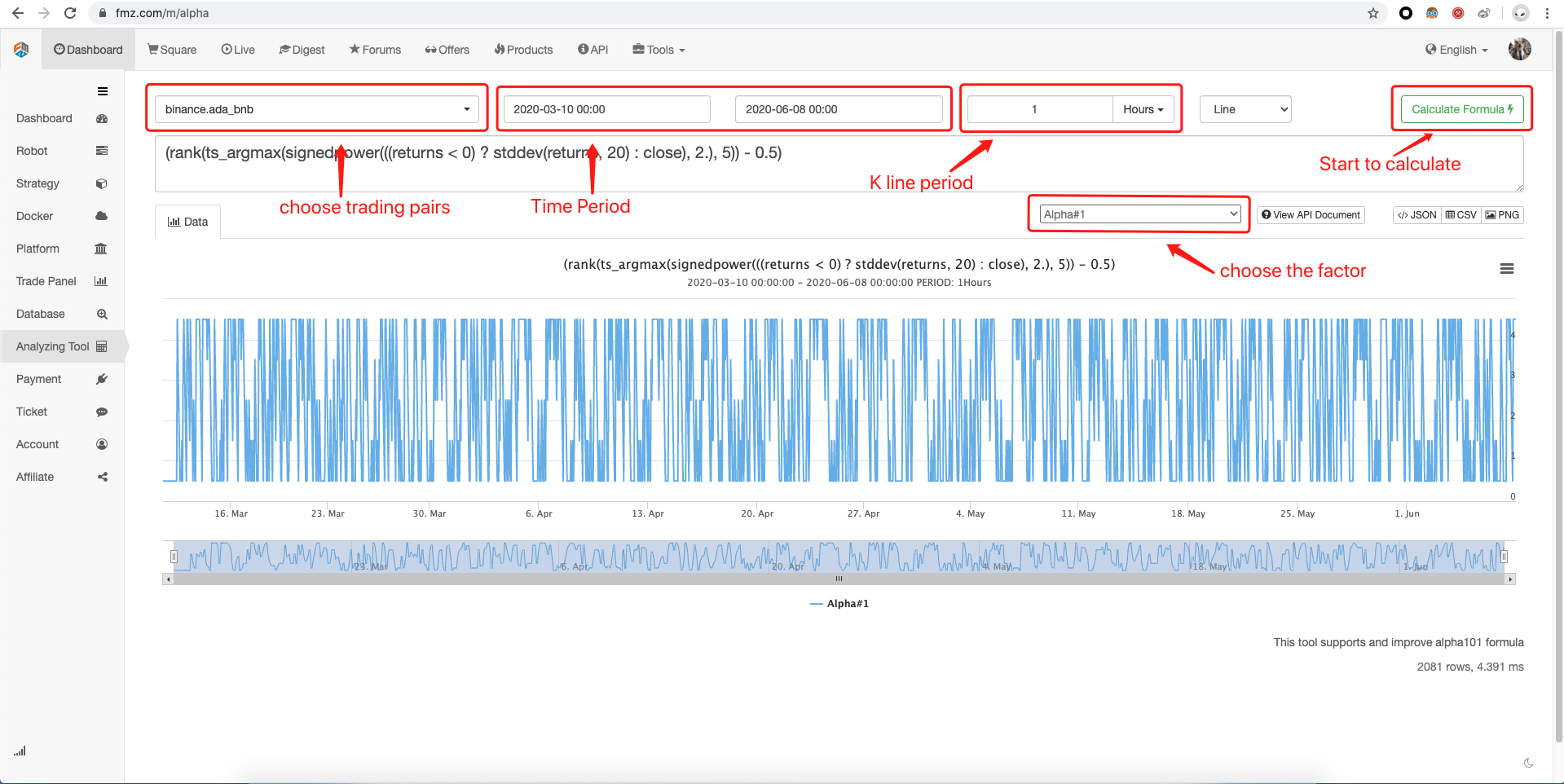
Open FMZ official website (FMZ.COM) to register and log in, click “Dashboard” on the upper left, and select “Analysis Tool” in the list on the left, as shown in the following figure:

On the analysis tool page, the top is the setting bar, which can be set in order from left to right: variety, start and end time, period, picture type. Below the settings bar is the formula editing area. If you can’t write formulas, you can click on the drop-down menu below and select the formula you have edited. There are many formula examples supported here. In addition, the FMZ platform analysis tools already support most of the official Alpha101 formulas, just click and use. Click the calculation formula to display the calculation results at the bottom, it supports multiple data export methods: pictures, tables (CSV), JSON, etc.
Need to pay attention to
The parameters in the factor formula are default and not the optimal parameters. Traders can choose the more appropriate parameters according to the symbol, period, and their own experience.
The factors are independent of each other, and superimposing multiple factors on each other may not necessarily result in better results. When designing quantitative trading strategies, at least have their own logic, not mechanical patchwork.
The factors are unlimited, Alpha101 is just a trick, I believe everyone can get inspiration from it and create more and better factors and quantitative trading strategies.
To sum up
In many trading factor formulas, the surface seems unreasonable, but there are certain ideas and reasons behind the formula. But the only constant in the market is that it is constantly changing, so the effectiveness of these factors has non-linear characteristics in practical applications. In other words, there is no effective and always effective factor, there is no universal trading method. As a quantitative trader, you should have an open mind, be good at summarizing, and use it to try and innovate to make profits in a constantly changing market.